Trigonometric Notes/Formulas

3 Comments / Blog / By

Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. It has widespread applications in fields such as physics, engineering, computer graphics, and even music theory. In this post, we’ll explore some essential trigonometric formulas, their derivations, and applications.

Basic Trigonometric Rules

\[ sin(θ)= \frac{Opposite side}{Hypotenuse}\] \[ cos(θ)= \frac{Adjacent side}{Hypotenuse}\] \[ tan(θ)= \frac{Opposite side}{Adjacent side} = \frac{sin(θ)}{cos(θ)}\]
\[ cot(θ)= \frac{Adjacent side}{opposite side} = \frac{cos(θ)}{sin(θ)}\] \[ sec(θ)= \frac{Hypotenuse}{Adjacent side} = \frac{1}{cos(θ)}\] \[ cosec(θ)= \frac{Hypotenuse}{Opposite side} = \frac{1}{sin(θ)}\]

Pythagorean Identities

\[sin^{2}(θ)+cos^{2}(θ)=1\] \[tan^{2}(θ)+1=sec^{2}(θ)\] \[cot^{2}(θ)+1=cosec^{2}(θ)\]

Double And Triple Angle Formula

\[ sin(2θ)= 2 sin (θ). cos(θ )\] \[\begin{array}{rcl} cos(2θ) & = & cos^2(θ)−sin^2(θ) \\ & = & 2cos^2(θ)−1 \\ & = & 1- 2sin^2(θ ) \end{array}\] \[tan(2θ)= \frac{2tanθ}{1-tan^2(θ)}\]
\[ sin(3θ)= 3sin (θ)- 4 sin^3(θ )\] \[cos(3θ) = 4 cos^3 (θ) – 3cos(θ) \] \[tan(3θ)= \frac{3tanθ – tan^3 (θ) }{1- 3tan^2(θ)}\]

Half Angle Formula

\[sin\frac{θ}{2} = \pm \sqrt{\frac{1-cosθ}{2}}\] ​\[cos\frac{θ}{2} = \pm \sqrt{\frac{1+cosθ}{2}}\] \[tan\frac{θ}{2}= \frac{sin θ }{1+cosθ}=\frac{1-cosθ }{sinθ}\]

Single Angle Formula

\begin{array}{rcl} sin θ & = & 2sin\frac{θ}{2}. cos\frac{θ}{2} & = & \frac{2tan\frac{θ}{2}}{1+tan^2\frac{θ}{2}} \\ \end{array}\] \begin{array}{rcl} cos θ & = & cos^2\frac{θ}{2}- sin^2\frac{θ}{2} \\ & = & \frac{1- tan^2\frac{θ}{2}}{1+tan^2\frac{θ}{2}} \\ & = & 2cos^2\frac{θ}{2}- 1 \\ & = & 1- 2sin^2\frac{θ}{2} \\ \end{array}\]

Angle Sum and Difference Formula

\[ sin(A+B)= Sin A. Cos B + Cos A . Sin B\] \[ sin(A-B)= Sin A. Cos B – Cos A . Sin B\] \[ Cos(A+B)= Cos A. Cos B – Sin A . Sin B\] \[ Cos(A-B)= Cos A. Cos B + Sin A . Sin B\]
\[tan(A+ B)= \frac{tanA+ tan B}{1-tanA . tan B}\] \[tan(A- B)= \frac{tanA- tan B}{1+tanA . tan B}\]

Product to Sum Formula

\[Sin A. Sin B = \frac{1}{2} [ Cos (A – B) – Cos(A + B)]\] \[Cos A. Cos B = \frac{1}{2} [ Cos (A + B) + Cos(A – B)]\] \[Sin A. Cos B = \frac{1}{2} [ Sin (A + B) + Sin(A – B)]\] \[Cos A. Sin B = \frac{1}{2} [ Sin (A + B) – Sin(A – B)]\]

Sum to Product Formula

\[sin A + Sin B = 2 Sin\frac{A+B}{2} . Cos\frac{A-B}{2}\] \[sin A – Sin B = 2 Cos\frac{A+B}{2} . Sin\frac{A-B}{2}\] \[Cos A + Cos B = 2 Cos\frac{A+B}{2} . Cos\frac{A-B}{2}\] \[Cos A – Cos B = – 2 Sin\frac{A+B}{2} . Sin\frac{A-B}{2}\]

Some other Derived Formulas

\[ 1 + cos(θ) = 2 cos^2\frac{θ}{2}\] \[ 1+ cos 2(θ) = 2 cos^2(θ)\]
\[ 1 – cos(θ) = 2 sin^2\frac{θ}{2}\] \[ 1- cos 2θ = 2 sin^2θ\]

Signs of trigonometric functions in different quadrants

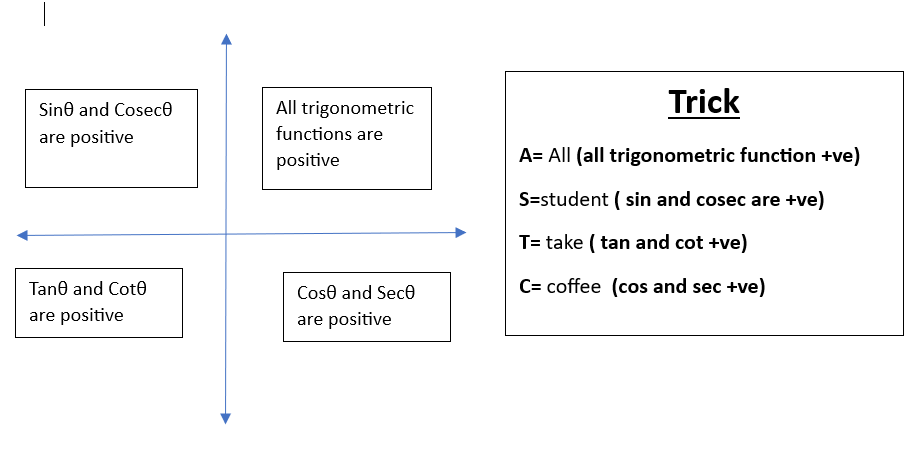
Trigonometric functions are foundational in mathematics, especially in the study of angles and triangles. Understanding the signs of these functions in different quadrants is crucial for solving problems in trigonometry, calculus, and physics. In this blog, we’ll explore how the signs of sine, cosine, tangent, and their reciprocals change depending on the angle’s position in the Cartesian plane.

Mnemonic to Remember the Signs

A popular mnemonic to help remember which functions are positive in each quadrant is “All Students Take Coffee.” Each word corresponds to a quadrant:
 

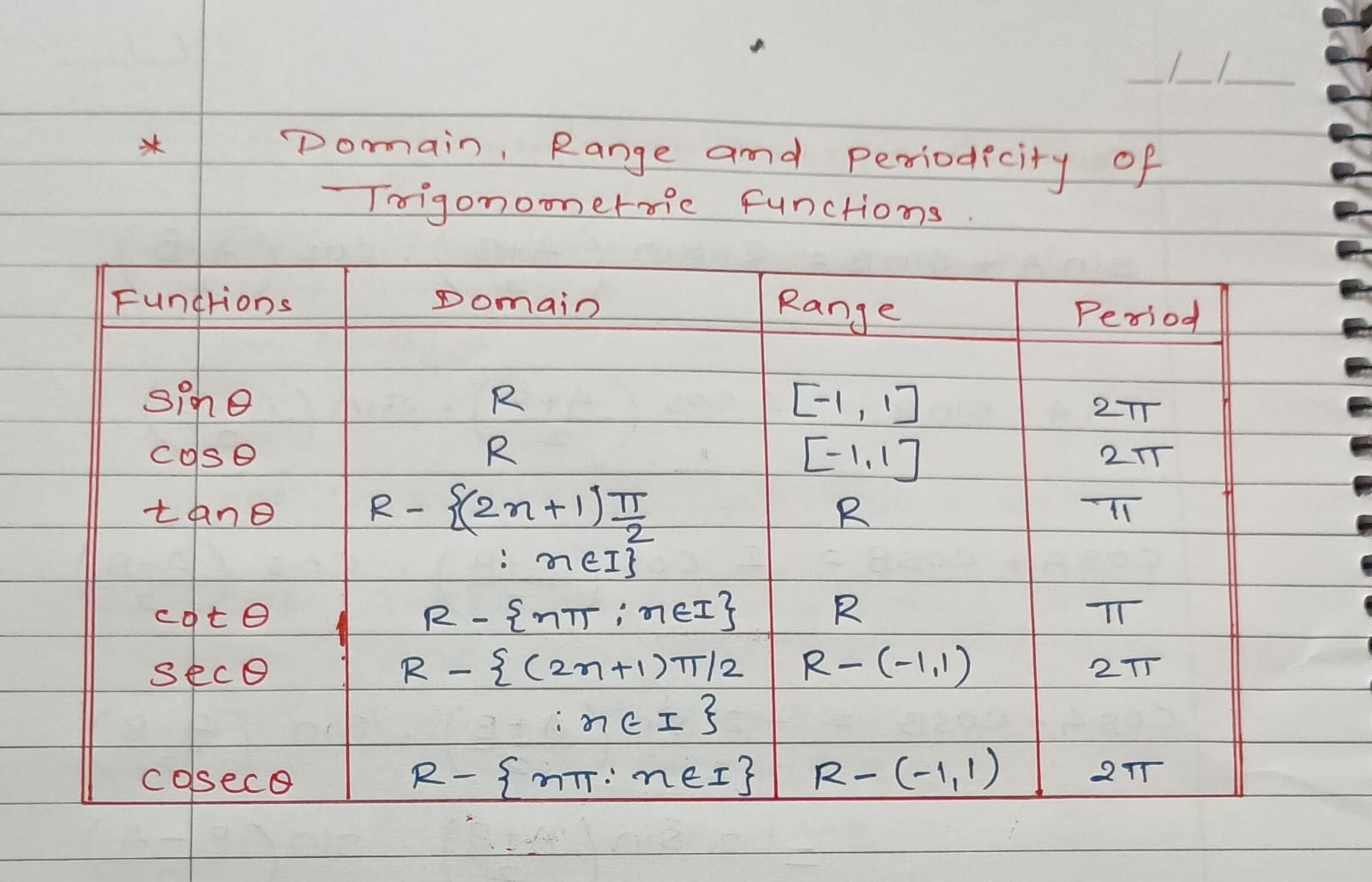
Domain, Range, and Periodicity of Trigonometric functions

Domain

The domain of a function is the set of all possible input values for which the function is defined.

 Range

The range of a function is the set of all possible output values that the function can produce when you input values from its domain. It shows the values that the function can take based on the inputs from the domain.

 Periodicity

A function is said to be periodic if it repeats its values at regular intervals, known as the period.. In trigonometric functions, this means they repeat their values over specific intervals (like 2 π   for sine and cosine, or  π for tangent and cotangent).

Trigonometric Functions of Allied Angles

What Are Allied Angles?

Among various concepts in trigonometry, the functions of allied angles play a significant role in simplifying calculations and solving problems.  we’ll explore what allied angles are, their properties, and how to calculate their trigonometric functions. Allied angles are two angles that add up to 90° (or π/2​ radians). 

For example, if one angle is 30°, its allied angle is 60°, since:

30°+60°=90°

Allied angles are often expressed as:

If A is an angle, then its allied angle is 90°−A.

Trigonometric Values

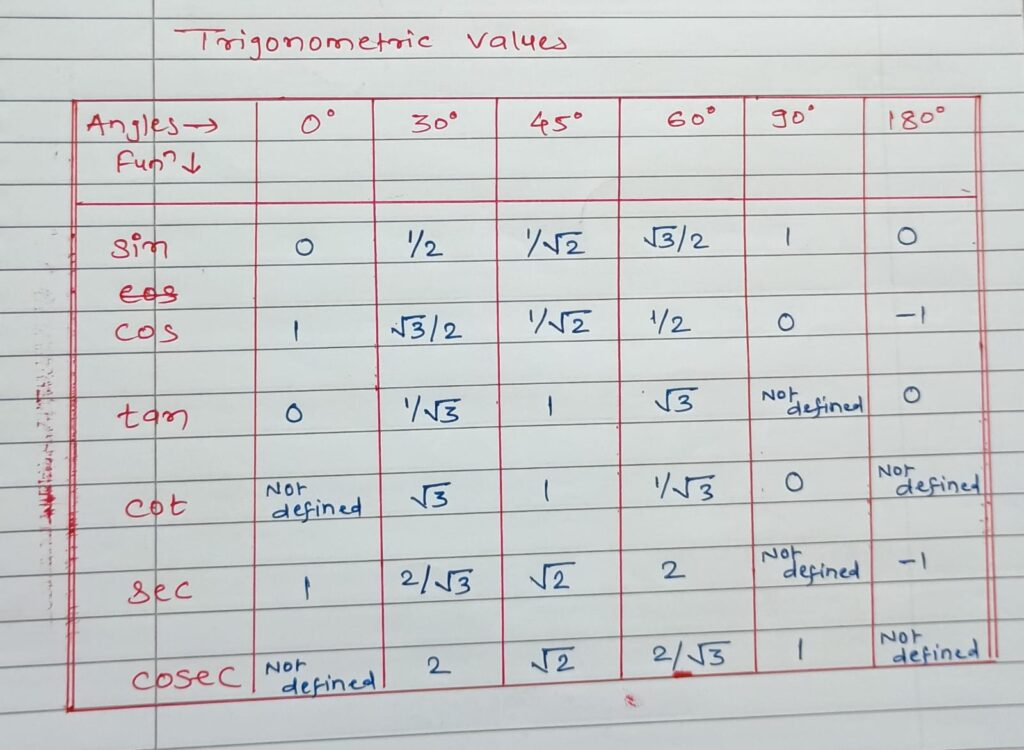
Trigonometric functions are fundamental in mathematics, especially in geometry and calculus. Knowing the trigonometric values for common angles can greatly simplify calculations in various fields, including physics, engineering, and computer science.  we will explore the sine, cosine, and tangent values for key angles.

PDF link of above trigonometric formulas Download

3 thoughts on “Trigonometric Notes/Formulas”

  2. Pingback: Class 12 CBSE/NCERT_ Mathematics - Study Snaps

Leave a Comment

Your email address will not be published. Required fields are marked *